註：本文同步更新在Notion!（數學公式會比較好閱讀）

每年都會聽到小大一們的哀號，希望微積分可以過

當然也會聽到，學了微積分以後不會用到幹嘛教

今天主要在微分跟矩陣微分，直接進入正題gogo

微分

基本微分公式

1. 常數項的微分
   

2. 冪法則 (Power Rule)
   

3. 指數函數的微分
   

4. 對數函數的微分
   

5. 三角函數的微分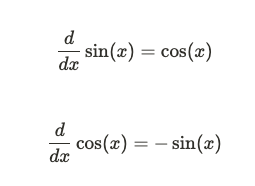
   

乘法與鏈式法則

• 乘法法則 (Product Rule)
  

• 鏈式法則 (Chain Rule)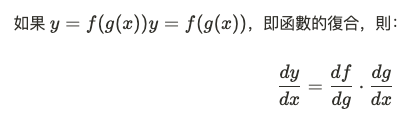
  
  鏈式法則在機器學習中反向傳播算法的推導中極其重要。

矩陣微分（Matrix Calculus）

矩陣微分是線性代數和微分計算的結合，特別是在處理向量和矩陣形式的函數時極為有用。它在機器學習中的優化過程中被廣泛使用，例如在反向傳播算法中計算權重的梯度時，矩陣微分很常使用到。

標量對向量的微分

這樣的微分結果可以直接應用於機器學習中的最小二乘法。

向量對向量的微分

矩陣對矩陣的微分

常見矩陣微分公式

應用：機器學習中的梯度下降法

在機器學習中，我們經常需要對損失函數（如均方誤差、交叉熵等）進行優化。梯度下降法是一種常用的優化技術，它基於損失函數對權重矩陣的微分（即梯度）。矩陣微分在這裡至關重要，因為我們處理的數據往往是向量或矩陣形式。

微積分就提到微分和矩陣微分，在處理高維數據、優化模型和計算梯度時就比較容易上手。無論是經典的二次型函數還是複雜的矩陣對矩陣的微分，都有助於我們了解模型的內在運行機制。

接下來會討論到 最佳化理論跟統計，我不希望大概把數學當成無聊的一項，所以我盡量會有趣（？）